In questa guida troverete le basi per capire come usare LINGO, la pagina è composta da una breve introduzione allo scopo del software, alcuni esempi di problemi risolti utilizzando le funzioni di base e infine una parte finale contenente tutte le istruzioni nel linguaggio LINGO: funzioni matematiche, operatori logici, ecc.
Introduzione a LINGO
A cosa serve LINGO?
Si tratta di un software dedicato alla risoluzione di problemi di ottimizzazione di diverse tipologie: programmazione lineare, quadratica e non lineare, vincolati da equazioni e/o disequazioni.
Il nome del software deriva da Linear INteractive and General Optimizer.
Il linguaggio di programmazione LINGO è molto semplice, infatti esso non comprende una grande varietà di funzioni, in questa guida parleremo delle funzioni più utilizzate.
Un problema di ottimizzazione è espresso da una funzione obiettivo (da massimizzare o minimizzare) e i vari vincoli imposti alle variabili della funzione (equazioni o disequazioni).
La funzione obiettivo può essere di varia natura, per fare alcuni esempi possiamo considerare un sistema di trasporto: in questo caso una possibile funzione obiettivo potrebbe essere il flusso dei veicoli uscenti dalla rete stradale, per la quale vogliamo ottenere il massimo valore.
L’editor permette anche l’inserimento di commenti all’interno del codice che appariranno in colore verde, mentre le funzioni saranno colorate in blu. Il resto del testo (le variabili e le operazioni) sarà in nero.
La sintassi per inserire un commento fa utilizzo di un punto esclamativo all’inizio di esso, come in questo esempio:
!Questo testo apparirà come commento;
Analizziamo ora, per cominciare questa guida a LINGO, un semplicissimo problema:
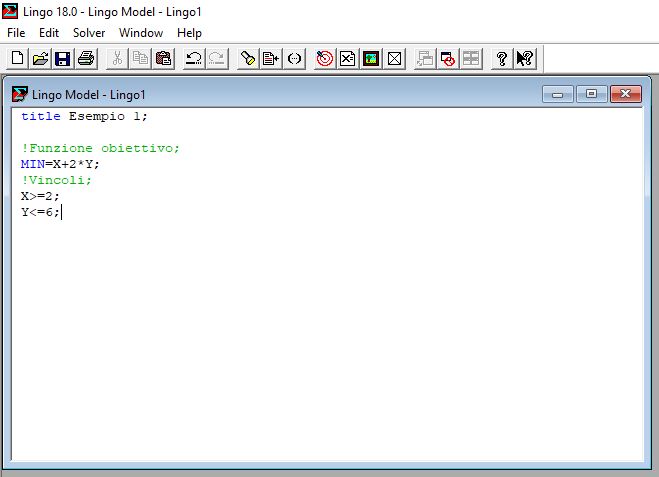
Primo Esempio
!Funzione obiettivo;
MIN=X+2*Y;
!Vincoli;
X>=2;
Y<=6;
Il problema qui rappresentato è già scritto facendo uso del linguaggio di programmazione LINGO, possiamo notare la grande somiglianza con la notazione matematica, caratteristica principale che rende facile e immediato l’utilizzo di questo programma.
In questo caso il programma fornirà come risultato del problema i valori di X e Y che forniscono il minimo della funzione X+2*Y, oltre che il valore minimo della funzione obiettivo.
Questo era l’esempio più semplice, ora vediamo ulteriori metodi di modellizzazione di problemi simili.
Ad esempio possiamo impostare un valore iniziale per le variabili.
INIT:
X=5;
Y=4;
END INIT
MIN=X^2-10*Y+C;
X>=2;
Y<=4;
DATA:
C=2;
END DATA
In questo caso oltre ad aver imposto un valore iniziale alle variabili X e Y, la costante C è stata dichiarata utilizzando il metodo di dichiarazione dei dati del problema in LINGO, trattandosi appunto di una costante e non di una variabile.
Funzioni di base in LINGO
Questa prima parte sulle basi di LINGO era necessaria per capire che tipologia di problemi può essere risolta dal software, adesso andremo a parlare delle funzioni che permettono di risolvere problemi più complessi, dall’ottimizzazione di reti di trasporto a problemi di ricerca operativa.
Gruppi di elementi (SETS)
La più utile e necessaria caratteristica del software LINGO è la possibilità di utilizzare una rappresentazione vettoriale di dati e variabili; permettendo così di sommare, eseguire iterazioni ed esprimere i vincoli per grandi insiemi di valori attraverso gli indici del vettore.
Gli insiemi (vettori) in LINGO devono essere dichiarati all’inizio del codice attraverso la seguente sintassi:
SETS:
Vettore1/1..5/: Valore1, Valore2, Valore3;
Vettore2/1..7/: Valore4, Valore5;
END SETS
Con queste righe è stato dichiarato un vettore di dimensione 5 e un vettore di dimensione 7, entrambi contententi due valori per ciascun indice.
Le funzioni principali utilizzate per lavorare su vettori di dati sono le seguenti:
@FOR permette di eseguire un’iterazione gli indici di un vettore, inoltre imponendo una condizione possiamo selezionare solamente un sottoinsieme di elementi del vettore.
@SUM permette di eseguire la somma degli elementi di un vettore.
@MIN calcola il valore minimo di un’espressione tra tutti gli elementi di un vettore.
@MAX calcola il valore massimo di un’espressione tra tutti gli elementi di un vettore.
Esempi:
- Funzione @FOR
@FOR(Vettore1(i): Valore3(i)=Valore1(i)+Valore2(i));
La funzione esegue la somma tra i valori Valore1 e Valore2 del Vettore1 e inserisce il risultato nella variabile Valore3, questo viene eseguito per ciascun indice del Vettore1 (quindi per 5 volte).
- Funzione @SUM
Somma = @SUM(Vettore1(i) | i#GE#2: Valore3(i));
La funzione esegue la sommatoria dei Valore3(i) contenuti nel Vettore1, solamente per i valori con indice i maggiore o uguale a 2 (#GE# sta ad indicare Greater or Equal).
Per sommare i valori per tutti gli indici: @SUM(Vettore1(i): Valore3(i));
- Funzione @MIN e @MAX
Minimo3 = @MIN(Vettore1(i): Valore3(i));
Massimo3 = @MAX(Vettore1(i): Valore3(i));
Le istruzioni precedenti calcolano semplicemente i valori minimo e massimo tra gli elementi Valore3 del Vettore1.
Funzioni annidate
Tutte le funzioni precedentemente elencate hanno possibilità di essere annidate per eseguire operazioni più complesse, come l’iterazione attraverso più indici (SETS multidimensionali).
Per chi non fosse pratico l’annidamento è semplicemente l’inserimento di un’istruzione all’interno di un’altra, tipicamente utilizzato per iterazioni su due variabili; proprio quello che faremo nel nostro esempio, usando due cicli @FOR annidati.
Ad esempio per generare variabili a più indici si possono considerare i seguenti sets:
SETS:
Links/1..5/: L, vmax;
TimeInt/1..5/: gamma;
LinksTime (Links, TimeInt): q_out_total;
END SETS
Questo esempio deriva da un problema di ottimizzazione di reti stradali, dove il set Links rappresenta i tratti stradali mentre TimeInt rappresenta gli intervalli di tempo per cui vogliamo calcolare il risultato. (Ignoriamo il significato di L, vmax e gamma, è irrilevante per il momento).
Può capitare che nella modellizzazione di un problema sia utile utilizzare un set dipendente da altri due sets, in questo caso per definire il flusso uscente totale (q_out_total) abbiamo bisogno di due indici, uno relativo al tratto di strada e uno relativo all’intervallo di tempo per cui il flusso uscente è stato calcolato.
Esempio: annidamento @FOR
Un esempio di funzione annidata utilizzabile per questa variabile è il seguente:
@FOR(TimeInt(t): q_out_total(1,t)=200);
@FOR(Links(i)|i#GE#2: @FOR(TimeInt(t)|t#GE#2: q_out_total(i,t)=q_out_total(i-1,t-1)*0.75));
La funzione di esempio non ha senso pratico, soprattutto se presa singolarmente, ma permette di capire la logica di annidamento delle funzioni in LINGO.
Il problema in questo esempio rappresenta una riduzione del numero dei veicoli progressiva del 25% in seguito al passaggio in ogni tratto di strada consecutivo percorso dalle auto.
Il primo ciclo @FOR impone un flusso di 200 (veicoli/ora) per il primo tratto stradale “Link(1)” che rimane costante per tutti e 5 gli intervalli di tempo.
In seguito, con il secondo ciclo di @FOR annidati, per ciascun tratto “Link(i)” (escluso il primo “i#GE#2”) e per ciascun intervallo di tempo “TimeInt(t)” (escluso il primo “t#GE#2”) impone che il flusso uscente dal tratto nell’intervallo di tempo sia di una frazione del 75% rispetto al tratto precedente “i-1” nell’intervallo di tempo precedente “t-1”.
Infatti i risultati sono i seguenti:
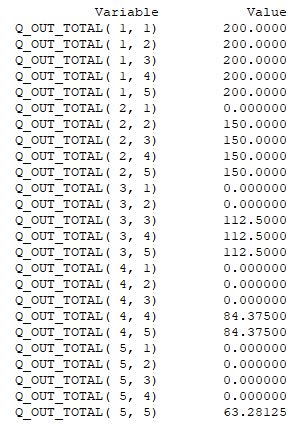
Nella soluzione, con la crescita degli indici delle variabili, si può notare una diminuzione del flusso del 25% in seguito al passaggio al tratto stradale e intervallo di tempo successivo, fino a un progressivo svuotamento della rete per la variabile (5, 5).
L’annidamento delle funzioni è uno strumento molto utile ed efficace in situazioni simili in cui ci troviamo ad analizzare valori dipendenti da più indici in un dominio a tempo discreto, e per questo è un passaggio chiave per imparare ad utilizzare LINGO.
Struttura del codice in LINGO
Per il momento abbiamo finito con la spiegazione delle basi del programma e avrai sicuramente capito come usare LINGO; adesso ricapitoliamo la struttura del codice necessaria al funzionamento di LINGO.
!Definizione delle variabili e/o degli insiemi;
SETS:
…
END SETS
!Funzione obiettivo;
MAX = … oppure MIN = …
!Vincoli;
…
!Dati del problema;
DATA:
…
END DATA
Soluzione del problema
Dopo l’avvio del programma la soluzione sarà fornita nella seguente forma:
Local optimal solution found.
Objective value: 422.4832
Total solver iterations: 81
Model Title: Exercise 1
Variable Value Reduced Cost
L(1) 4.000000 0.000000
L(2) 5.000000 0.000000
L(3) 2.000000 0.000000
L(4) 3.000000 0.000000
L(5) 5.000000 0.000000
Queste diciture rappresentano il valore finale della funzione obiettivo (Objective value), il numero di iterazioni necessarie, il quale può essere ridotto in seguito inizializzando le variabili con valori vicini al loro valore finale, e infine i valori di tutte le variabili utilizzate nel problema (in questo caso ho riportato soltanto le prime 5).
Altre funzioni utili e operatori in LINGO
In quest’ultima parte troviamo le funzioni e gli operatori necessari per programmare in LINGO.
Funzioni utilizzabili per specificare alcune variabili
Nota: Tutte le variabili “X” inizializzate senza una delle seguenti funzioni saranno considerate di default X ≥ 0
@BND(estremo_inf, X, estremo_sup) INF <= X <= U
@BIN(X) X appartiene a B
@FREE(X) variabile libera X (esempio: nessuna restrizione di segno)
@GIN(X) X appartiene a N
Funzioni matematiche
@ABS(X) Valore assoluto di X.
@COS(X) Coseno di X (X in radianti).
@EXP(X) Esponenziale di X.
@LOG(X) Logaritmo naturale di X.
@SIGN(X) La funzione restituisce -1 se X<0 +1 se X >= 0.
@SIN(X) Seno di X (X in radianti).
@SIZE(nome_set) Fornisce il numero di elementi nel SET specificato.
@SMAX(list) La funzione restituisce il valore maggiore nella lista.
@TAN(X) Tangente di X (X in radianti).
Operatori logici
#EQ# = #NE# ≠
#GT# > #GE# ≥
#LT# < #LE# ≤
#AND# #OR# #NOT#
